Μια σπειροειδής σκάλα χρησιμοποιείται συνήθως για εσωτερική επικοινωνία μεταξύ των δωματίων που βρίσκονται σε διαφορετικούς ορόφους. Οι σπειροειδείς σκάλες γίνονται όπου πρέπει να εξοικονομήσετε χώρο. Το πλάτος των πορειών για μια σπειροειδή σκάλα είναι πιο λογικό να μην υπερβαίνει τα 0,95 μ.
Ο υπολογισμός μιας σπειροειδούς σκάλας έχει ως εξής. Ας υποθέσουμε ότι θέλετε να σχεδιάσετε μια σπειροειδή σκάλα με πλάτος S = 0,8 m και ύψος H = 3 m. Κατ 'αρχάς, προσδιορίζουμε τη συνολική διάμετρο της σπειροειδούς σκάλας D, η οποία ισούται με το άθροισμα του διπλού πλάτους των πτήσεων και του πάχους (διάμετρος) της κεντρικής στήλης στήριξης. Για παράδειγμα, αν η ξύλινη στήλη στήριξης έχει πάχος = 0,2 m, τότε η διάμετρος της σπειροειδούς σκάλας είναι D = 2xS + b = 2xO, 8 + 0,2 = 1,8 m.
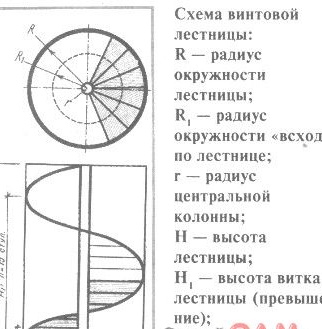
Από το κέντρο των σκαλοπατιών (Εικ.), Περιγράφουμε έναν κύκλο με ακτίνα R = D: 2 = 0,9 m και σχεδιάζουμε μια κεντρική στήλη με ακτίνα r = 0,1 m. = 0,5 m περιγράφουν έναν κύκλο που αντιπροσωπεύει την προβολή της γραμμής βλαστών στο σχέδιο μιας σπειροειδούς σκάλας. Για να προσδιορίσουμε τον αριθμό των βημάτων n ανά στροφή της σκάλας, διαιρούμε την περιφέρεια σε μέρη ίσα με το επιθυμητό πλάτος (βάθος) του βήματος s κατά μήκος της γραμμής βλαστών. Για παράδειγμα, πάρτε το πλάτος βήμα κατά μήκος της γραμμής βλαστών s = 0,2 m. Στη συνέχεια, ο αριθμός των βημάτων είναι n = 2xPR1: s = 2x3,14x0,5: 0,2 = 15.
Διαχωρίστε τον κύκλο σε n μέρη (στην περίπτωση αυτή, 15) και τραβήξτε ακτινικές γραμμές.
Έτσι, όταν σκαρφαλώνει πάνω και κάτω την σπειροειδή σκάλα, ένα άτομο κινείται ελεύθερα, χωρίς να χτυπάει το κεφάλι του στην εσωτερική πλευρά των βημάτων, είναι απαραίτητο να υπερβεί το H1 του 15ου βήματος πάνω από το 1ο, που αντιστοιχεί στην ανάπτυξη του μέσου ατόμου ή ακόμα περισσότερο. Για παράδειγμα, ας πάρουμε ύψος ενός ατόμου ίσο με 1,9 μ. Επιπλέον, θα πρέπει να προστεθεί στην αύξηση αυτή η "ανάπτυξη" (0,2 m) και το πάχος βήματος (0,05 m), αν γίνουν βήματα από μια "πενήντα" σανίδα. Έτσι, η υπέρβαση του 15ου βήματος πάνω από το 1ο θα είναι ίση με το άθροισμα της ανάπτυξης του ατόμου, του "αποθέματος" και του πάχους του βήματος. Δηλαδή, H1 = 1.9 + 0.2 + 0.05 = 2.15 m.
Διαχωρίζοντας το ύψος της πλήρους στροφής με τον αριθμό των βημάτων (n = 15), λαμβάνουμε το ύψος ενός σταδίου h = H1: n = 2.15: 15 = 0.14 m.
Ο συνολικός αριθμός των βημάτων μιας σπειροειδούς σκάλας καθορίζεται διαιρώντας ολόκληρο το ύψος των σκαλοπατιών κατά το ύψος ενός σταδίου. Στην εξεταζόμενη περίπτωση, στο Η = 3 m, ο συνολικός αριθμός των βημάτων είναι η = 21, και ο αριθμός των πέλμων, αντίστοιχα, είναι η - 1 = 21-1 = 20.
Το ανεπαρκές πλάτος του πέλματος στην σπειροειδή σκάλα μπορεί να αντισταθμιστεί από την προεξοχή στα σκαλοπάτια. Η "προεξοχή" της προεξοχής ενός βήματος δεν πρέπει να υπερβαίνει τα 0,09 m.
Για τη διευκόλυνση της αναρρίχησης μιας σπειροειδούς σκάλας, η διάμετρος της μεσαίας στήλης συνήθως αυξάνεται, ως αποτέλεσμα της βαθμίδας, λαμβάνεται ένα τραπεζοειδές σχήμα, ενώ το πλάτος της βαθμίδας του εσωτερικού άκρου αυξάνεται.
Η κατεύθυνση εισόδου και εξόδου από τις σκάλες σε αυτή την περίπτωση (με n = 21) δεν θα συμπίπτει.
